Projects description

Purpose: This is my notes for the approximation methods of marching, including explicit Euler method, implicit Euler method, implicit midpoint, and Runge-Kutta method.

Reference: Some part of this notes is based on the book “Numerical Methods for Computational Science and Engineering”

Problem description

That is, the initial conditions and the differential equation (time derivative) are given, then the solution can be given by time marching.

$$\mathbf {\dot{y}}=\mathbf{f}(t,\mathbf{y}),\space{} \mathbf{y(t_0)}=\mathbf{y_0}$$ We can calculate the $\mathbf{y}$ on a temporal mesh covering the time interval between initial time $t_0$ and final time $T$.

$$(\mathbf{y}^{n},h^{n}) \mapsto \mathbf{\Psi}(\mathbf{y}^{n},h^{n})=\mathbf{y}^{n+1}$$ $\mathbf{\Psi}$ stands for the operator of discretization.

其实所有的时间推进如果按相似的离散方式表示，均为： 下个时间步结果=上个时间步的数据+时间步长*斜率，接下来即将介绍的各种方法的区别仅为对斜率的构造方法不同。

$$\begin{aligned} & \frac{y^{n+1}_i-y^{n}_i}{dt}=\mathbf{f}(t,\mathbf{y}) \ & \Rightarrow y^{n+1}_i=y^{n}_i+dt*\mathbf{f}(t,\mathbf{y}) \end{aligned}$$

Method descrition

Assuming $$h_n=t_{n+1}-t_n$$ The $\mathbf{\dot{y}}$ stands for the differential $\mathbf{y}$ with time, $\mathbf{y}$ is the value tensor, $y_i$ is the i components.

In this note, the subscript($a_i$) stands for the spatial discretization and the superscript($a^n$) stands for the time discretization.

Explict Euler method

Explict Euler method is based on forward difference quotient:

$$\mathbf{\dot{y}}=\mathbf{f}(t,\mathbf{y})\longleftrightarrow \underbrace{\frac{\mathbf{y}^{n+1}-\mathbf{y}^{n}}{h_n}}_{Forward \space{} difference}\approx \mathbf{f}(t_n,\mathbf{y^{n}}), n=0,1,2,..,N-1$$

$$\begin{aligned} &\Rightarrow \frac{y^{n+1}_i-y^{n}_i}{h_n}=\mathbf{f}(t_n,y_i^{n}) \ & \Rightarrow y^{n+1}_i=y^{n}_i+h_n*\mathbf{f}(t,y_i^{n}) \end{aligned}$$

说明： 显然，此时未知数仅是$y^{n+1}_i$，而等式右边的均为已知数，故直接通过等式求出未知数，进行时间推进即可。

对于CFD问题，$\mathbf{f}$通常是一个与物理量相关的空间离散量，通过初始条件、边界条件，能够得到全场在初始时刻的各物理信息，即能获得等式右边的值，而基于该结果，进行计算，即可获得下一个时刻的物理量，以此进行时间推进。

理解： 由图可知，此时的斜率是在$(t_0,y_0)$取得的，基于该斜率估算下一个时间步结果，如果dt较大，将会带来显著误差。

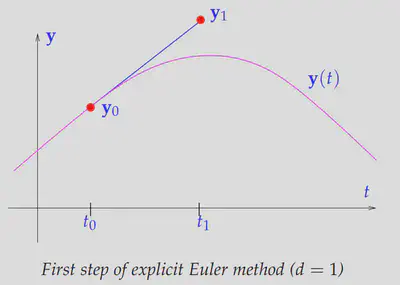
优劣： 推导简单，编程简单，且利于并行，但容易耗散，需要小时间步长(CFL) 简单说"小步快走易并行"

Implicit Euler method

Implicit Euler method is based on backward difference quotient:

说明: 显然，此时等式左右两边均出现了未知数$y^{n+1}_i$，由于$\mathbf{f}$是已知的，故通常做法是将等式右边的$y^{n+1}_i$移到等式左边，再经过变形，获得一组方程组，联立方程组进行求解。

理解： 此时的斜率是在$(t_1,y_1)$取得的，故能够对$y_1$进行较好地还原，但该斜率暂时是未知的，故唯一的问题是需要求解方程组获得

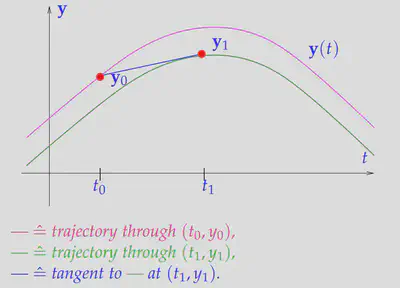
优劣： 推导较为复杂，编程复杂，且容易出现非线性(例如某个参数也是时间相关的，该参数乘上时间突进的物理量，将使得未知量的维度变为2)，加大了求解的难度，且不利于并行，但不容易耗散，可以大时间步长(CFL) 简单说"大步慢走难并行"

Implicit midpoint

Implicit midpoint method is based on a symmetric difference quotient, $$\mathbf{\dot{y}}=\mathbf{f}(t,\mathbf{y})\longleftrightarrow \underbrace{\frac{\mathbf{y}^{n+1}-\mathbf{y}^{n-1}}{2h_n}}_{Symmetric \space{} difference}, n=0,1,2,..,N-1$$

Then apply this formula in $t=\frac{1}{2}(t_k+t_{K+1})$

理解： 此时的斜率是在在$(t^,y^)$取得的，该点依然是未知的，但是基于已知和位置点共同构造的（暂时不知道好处在哪里）

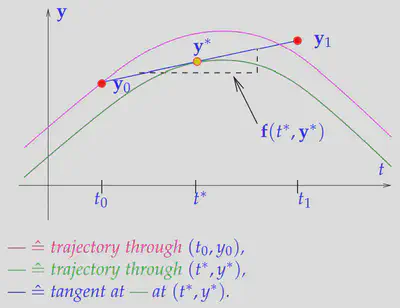
Runge-Kutta method

欧拉显示和欧拉隐式的精度都是一阶，而Runge-Kutta通过几次构造半时间步，获得了四阶精度，但龙格库塔本质上还是一个显示方法，并不涉及任何方程组的求解，可以理解为通过四次构造斜率，使得斜率最接近真实值

$$ \mathbf{y}^{n+1}=\mathbf{y}^{n}+\frac{dt}{6}(k_1+2k_2+2k_3+k_4) $$

$$ k_1=\mathbf{f}(t_n,\mathbf{y}_n) $$ $$ k_2=\mathbf{f}(t_n+\frac{dt}{2},\mathbf{y}_n+\frac{dt}{2}k_1) $$ $$ k_3=\mathbf{f}(t_n+\frac{dt}{2},\mathbf{y}_n+\frac{dt}{2}k_2)$$ $$ k_4=\mathbf{f}(t_n+dt,\mathbf{y}_n+dtk_3)$$

Case: simple function

Description

Take this simple function as an example to demonstrate how those methods work.

$$\mathbf{\dot{y}}=y, y^0=1$$ Obviously, this function has exact solution. $$y=y^0+e^{t}$$

For explict method: $$y^{n+1}=y^n+dt*y^n$$

For implict method: $$y^{n+1}=y^n+dt*y^{n+1}\longrightarrow y^{n+1}=\frac{y^n}{1-dt}$$

For implict midpoint method: $$y^{n+1}=y^n+dt*\frac{y^{n+1}+y^{n}}{2} \longrightarrow y^{n+1}=\frac{1+\frac{1}{2}dt}{1-\frac{1}{2}dt}y^n$$

For Runge-Kutta-4 method:

$$ \mathbf{y}^{n+1}=\mathbf{y}^{n}+\frac{dt}{6}(k_1+2k_2+2k_3+k_4) $$

$$ k_1=\mathbf{f}(t_n,\mathbf{y}_n) $$ $$ k_2=\mathbf{f}(t_n+\frac{dt}{2},\mathbf{y}_n+\frac{dt}{2}k_1) $$ $$ k_3=\mathbf{f}(t_n+\frac{dt}{2},\mathbf{y}_n+\frac{dt}{2}k_2)$$ $$ k_4=\mathbf{f}(t_n+dt,\mathbf{y}_n+dtk_3)$$

In this code, explict method, implict method, implicit midpoint and the exact solution have been calculated and presented in figure.

Code

# -*- coding: utf-8 -*-
"""
Created on Mon Sep 12 16:05:01 2022

@author: Howw
"""
import numpy as np
import matplotlib.pyplot as plt

step=40
dt=.1

y_explict=np.zeros([step])
y_exact=np.zeros([step])
y_implict=np.zeros([step])
y_mid=np.zeros([step])
y_runge=np.zeros([step])

y_explict[0]=1
y_implict[0]=1
y_mid[0]=1
y_exact[0]=1
y_runge[0]=1

def result(y):
    return y;

#Exact solution
for i in range(1,step):
    y_exact[i]=y_exact[0]*np.exp(i*dt)

#Explicit Euler
for i in range(1,step):
    y_explict[i]=y_explict[i-1]+dt*result(y_explict[i-1])
    
#imexplicit Euler
for i in range(1,step):
    y_implict[i]=y_implict[i-1]/(1-dt)
    
#Implicit midpoint
for i in range(1,step):
    y_mid[i]=((1+1/2*dt)/(1-1/2*dt))*y_mid[i-1]

#Runge-Kutta
for i in range(1,step):
    k1=y_runge[i-1]
    k2=y_runge[i-1]+k1*dt/2
    k3=y_runge[i-1]+k2*dt/2
    k4=y_runge[i-1]+k3*dt
    y_runge[i]=y_runge[i-1]+dt/6*(k1+2*k2+2*k3+k4)

    
plt.plot(y_explict,".",label="Explict")
plt.plot(y_implict,"*",label="Implict")
plt.plot(y_exact,label="Exact")
plt.plot(y_mid,"s",label="Mid")
plt.plot(y_runge,"+",label="Mid")
plt.legend()
plt.savefig("./result.png",dpi=100,bbox_inches="tight")