DeepONet
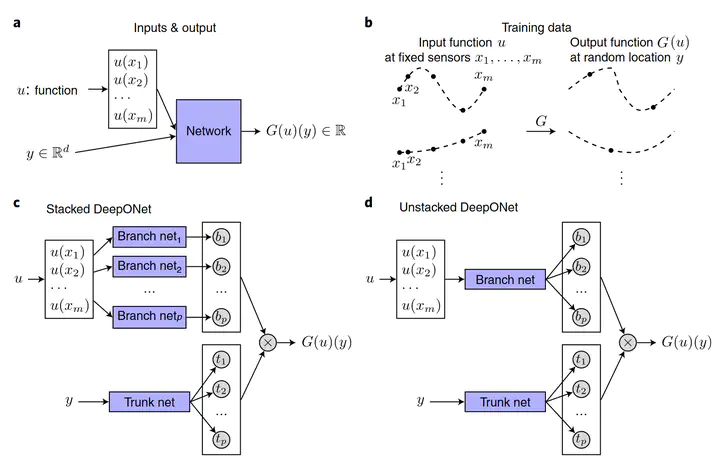 Photo from original paper
Photo from original paper1. 算子介绍 Operator Learning
1.1 传统方法
通用近似定理(Universal Approximation Theorem):即神经网络有能力以任意精度逼近任意连续函数。 比如我们想逼近 $y=x^2$ 这个函数,只需要准备一个二元组结构的数据集(x,y),其中x作为input,比如分别采样(0,1,2,3,4,5,6),而y作为label,给(0,1,4,9,16,25,36),这样数据集就变成了(0,0),(1,1),(2,4),(3,9),(4,16),(5,25)和(6,36)。喂给神经网络做训练至收敛,即能让神经网络在 $x \in [0,6]$ 这个区间中逼近$x^2$ ,在这一场景下,写成形式化的语言如下
$$\left|x^{2}-f_{n e t}(x)\right|<\epsilon$$
不论是PINNs模型还是传统的data-driven模型都是通过逼近函数的方法去解决问题。 此处学习到的,其实只是输入数组,数与数之间的关系,超出训练所用x的范围后,可能就会造成误差。
1.2 算子
扩展后的通用近似定理:单隐含层的神经网络可以准确逼近非线性连续泛函和非线性算子。 有了这个理论支撑,可以跳出逼近函数,而通过逼近算子去解决问题。
理论支持:根据论文[1],DeepONet的本质就是基于拓展通用近似定理在网络层面做一些修正,仍然是一个基于单隐含层神经网络的非线性算子通用逼近器。
关于算子(operator),引用维基百科的一段定义:
“在数学领域里,算子(operator)有别于物理的算符,是一种映射,一个向量空间的元素通过此映射(或模)在另一个向量空间(也有可能是相同的向量空间)中产生另一个元素。”
首先算子是一个映射关系。 其二是它作用于向量空间。这里需要解释一下向量空间及其notation,以一个n维向量空间 $\boldsymbol{R}^{n}$ 为例,它由所有的 n 维向量 v 组成,向量中的每个元素都是实数。如果n=2,则由所有2维向量(x,y)组成,用不那么严谨的大白话来讲就是二维向量空间是由平面上的所有点组成。也就是说算子是能作用在整个向量空间上的一种映射规则,而不是作用于具体的数。
例如那个 $y=x^2$ 的问题上,算子学习的目标是学习“平方”这个算子,进而实现输入任意x都能得到 $x^2$ 这一输出,这样的话泛化能力就远大于前面提到的逼近函数的方法,也从本质上学习到了这个方程本身。
1.3 算子具体实现
而应该给神经网络输入什么和设置它的输出是什么才能实现学到的是算子而不是函数呢? 以一个具体的实例来讲讲DeepONet到底让神经网络在学习什么: 以下面这个动力系统为例: $$ \frac{\mathrm{d} s(x)}{\mathrm{d} x} =u(x) \text{ } \text {and}\text{ } G: u(x) \mapsto s(x) \tag{1.1}$$ $$ s(x)=s_{0}+\int_{0}^{x} u(\tau) \mathrm{d} \tau, x \in[0,1] \tag{1.2}$$ 显然,原函数是$s(x)$,而$u(x)$是其常微分函数,数值解法如(1.2)所示。 而对于神经网络,尝试将常微分函数作为模型的输入 $u(x)$ ,给定一组坐标点 $y$ ,让神经网络能输出动力系统解的值 $s(y)$,即训练一个神经网络模型,能泛化到针对任意 $u(x)$ 的形态都适用。
而DeepONet解决的正是该问题。
2. DeepONet 实现

2.1 Inputs and Outputs
上图a展示的就是输入输出的情况,图b则展示了具体的输入输出。
输入:$[u(x1), u(x2), …, u(xm)]$ 和 $y$。
对输入的理解:$[u(x1), u(x2), …, u(xm)]$ 通过对$u(x)$取不同点进行采样,获取输入空间V中函数的不同表示,而$y$则是用于最终输出的,$y$的维度可以和$xm$不同。注意,对于每个输入函数$u$,都要求其在相同的$[(x1), (x2), …, (xm)]$上进行取值。
输出:$G(u)(y)$
对输出$G(u)(y)$的理解:$G$就是算子,其输入是函数$u(x)$,则$G(u)$就相当于输出函数,$G(u)(y)$就是输出函数在$y$处的结果。即$y$就是算子$G$在作用于函数$u(x)$时的自变量,而 $G(u)(y)$ 即是算子 $G$ 在作用于函数 $u(x)$ 时代入具体自变量 $y$ 后对应的值。它可以也可以不和 $x$ 的位置相同,其具体的取值和数量不受限制。
2.2 网络结构
上图c,d分别展示了stacked和unstacked两种不同结构的网络。
$$G(u)(y)\approx \sum_{k=1}^{p} \underbrace{b_k(u(x_1),u(x_2),…,u(x_m))}_{branch} \underbrace{t_k(y)} _{trank} \tag{2.1}$$
2.2.1 Stacked DeepONet
如图c所示,对于stacked DeepONet,有p个branch层平行堆叠,其处理输入的$[u(x1), u(x2), …, u(xm)]$。输入的$[u(x1), u(x2), …, u(xm)]$经过p个branch层后,成为p维的输出($b_k$)。每个branch是宽度为n的一个隐藏层网络
对于$y$则是通过trunk层处理,trunk是一层宽度为p的网络。即虽然trunk只有一层,但是其输出的$t_k$维度是$p$,即和branch层的输出维度是一样的。
最终将$b_k$与$t_k$点乘,作为最终网络的输出。
其实,该trunk-branch(主干-分支网络)也可以看作是一个trank网络,其最后一层的每个权值由另一个branch网络参数化,而不是传统的单变量。
说明:根据作者论文[1],P至少是10阶的(page 3),使用大量的分支网络是低效的
2.2.2 Unstacked DeepONet
可以认为其实和Stacked DeepONet相同,只是其每一个branch使用了相同的参数,则本质上就只剩下一个brunch
2.3 数据生成
(未完待续)
Refference
- Lu, L., Jin, P., Pang, G., Zhang, Z., Karniadakis, G.E., 2021. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat Mach Intell 3, 218–229. https://doi.org/10.1038/s42256-021-00302-5